Recently I've been studying the semantics of WebAssembly (wasm). If you've never heard of WebAssembly, it's a new web programming language that's planned to be a low-level analogue to JavaScript that's supported by multiple browsers. Wasm could be used as a compilation target for a variety of new frontend languages for web programming.
(see also Lin Clark's illustrated blog series on WebAssembly for a nice introduction)
As a cross-browser effort, the language comes with a detailed independent specification. A very nice aspect of the WebAssembly spec is that the language's semantics are specified precisely with a small-step operational semantics (it's even a reduction semantics in the style of Felleisen and Hieb).
A condensed version of the wasm semantics was presented in a 2017 PLDI paper written by Andreas Hass and co-authors.
(the current semantics of the full language is available at the WebAssembly spec website)
In this blog post, I'm going to share some work I've done to make an executable version of the operational semantics from the 2017 paper. In the process, I'll try to explain a few of the interesting design choices of wasm via the semantics.
A good thing about operational semantics is that they are relatively easy to understand and can be easily converted into an executable form. You can think of them as basically an interpreter for your programming language that is specified precisely using mathematical relations defined over a formal grammar.
Specifying a language in this way is helpful for proving various properties about your language. It's also an implementation independent way to understand how programs will evaluate, which you can use to validate a production implementation.
Because of the way that operational semantics resemble interpreters, you can construct executable operational semantics using domain specific modeling languages designed for that purpose (Redex, K, etc).
(Note: wasm already comes with a reference interpreter written in OCaml, but it's not using a modeling language in the sense described here)
The modeling language I'll use in this blog post is Redex, a DSL hosted in Racket that is designed for reduction semantics.
Why Make an Executable Formal Semantics?
If you're not familiar with semantics modeling tools, you might be wondering what it even means to write an executable model. The basic process is to take the formal grammars and rules presented in an operational semantics and transcribe them as programs written in a specialized modeling language. The resulting interpreters can be used to run examples in the modeled language.
The advantage to the executable model is that you can apply software engineering principles like randomized testing on your language semantics to see if there are bugs in your specification.
Another benefit that you get is visualization, which can be helpful for understanding how specific programs execute.
For example, here's a screenshot showing a trace visualization for executing a factorial program in wasm:
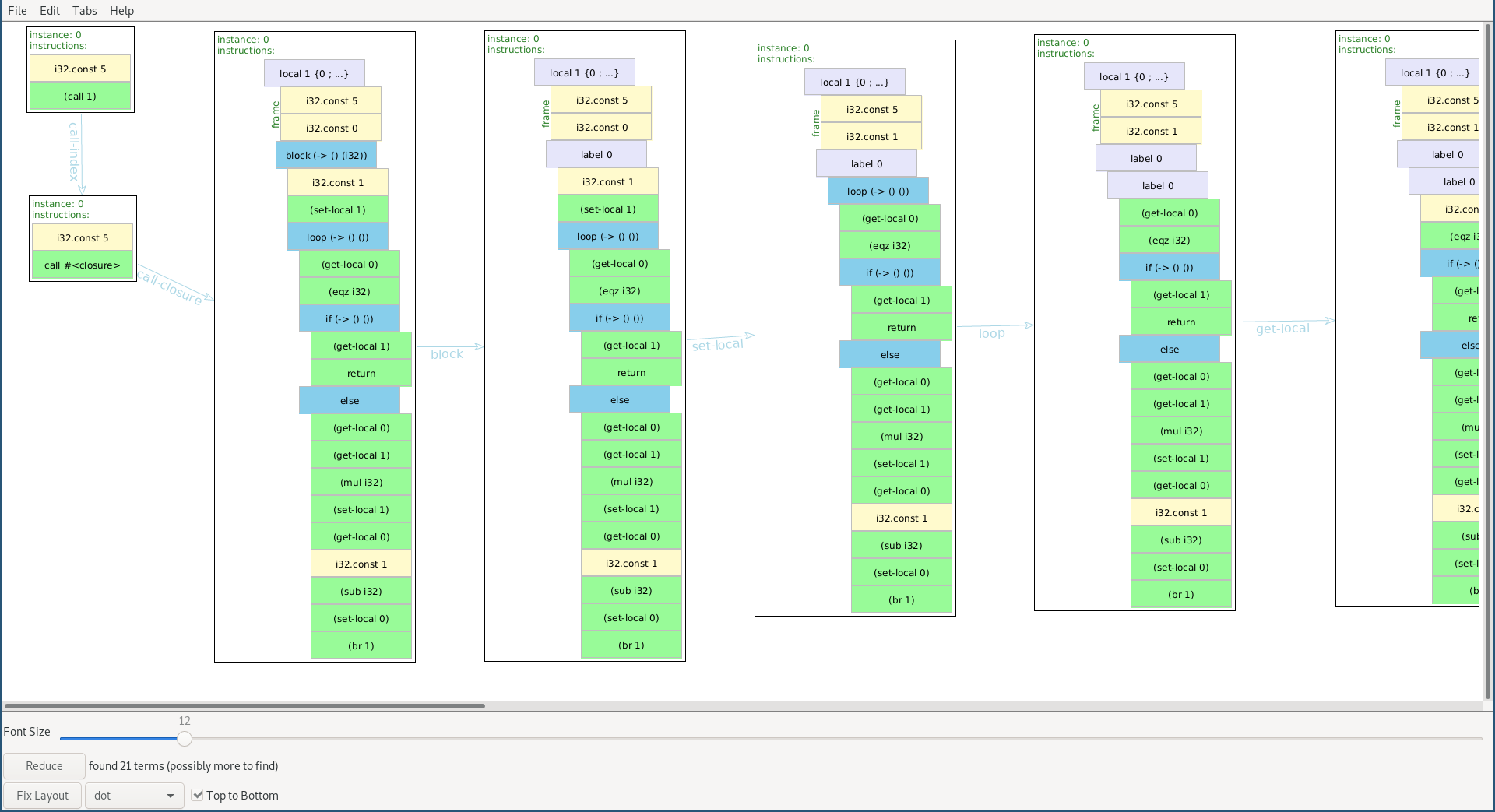
This is a custom visualization that I made leveraging Redex's built-in
traces
function, which lets you visualize every step of the reduction process. Here it shows a trace starting with a
function call to an implementation of factorial. Each box show a visual representation of the instructions
for that machine state. The arrows show the order of reduction, and which rule was used to produce
the next state.
In the next section I'm going to go over some background about semantics and modeling in Redex that's needed to understand how the wasm model works (you can skip this if you already familiar with operational semantics and Redex).
Redex & Reduction Semantics Basics
As mentioned above, the basic idea of reduction semantics is to define a kind of formal interpreter for your programming language. In order to define this interpreter, you need to define (1) your language as a grammar, and (2) what the states for the machine that runs your programs looks like.
In a simple language, the machine states might just be the program expressions in your language. But when you start to deal with more complicated features like memory and side effects, your machine may need additional components (like a store for representing memory, a representation of stack frames, and so on).
In Redex, language definitions are made using the define-language
form. It defines a grammar for your language using a straightforward pattern-based language that
looks like BNF.
A simple grammar might look like the following:
(define-language simple-language
;; values
(v ::= number)
;; expressions
(e ::= v
(add e e)
(if e e e))
;; evaluation contexts
(E ::= hole
(add E e)
(add v E)
(if E e e)))
The define-language form takes sets of non-terminals (e.g., e or v)
paired with productions for terms in the language (e.g., (add e e)) and
creates a language description bound to the given name (i.e., simple-language).
This is a small and simple language with only conditionals, numbers, and basic
addition. It accepts terms like (term 5), (term (+ (+ 1 2) 3)), (term (if 0 (+ 1 3) (if 1 1 2))) and so on.
(term
is a special Redex form for constructing language terms)
In order to actually evaluate programs, we will need to define a reduction relation, which describes how machine states reduce to other states. In this simple language, states are just expressions.
Here's a very simple reduction relation:
(define simple-red-v0
(reduction-relation simple-language
;; machine states are just expressions "e"
#:domain e
(--> (add v_1 v_2) ; pattern match
,(+ (term v_1) (term v_2)) ; result of reduction
;; this part is just the name of the rule
addition)
;; two rules for conditionals, true and false
(--> (if 1 e_t e_f) ; the _ is used to name pattern occurences, like e_t
e_t
if-true)
(--> (if 0 e_t e_f) e_f
if-false)))
You can read this reduction-relation
form as describing a relation on the states
e of the language, where the --> clauses define specific rules.
Each --> describes how to reduce terms that match a pattern, like (add v_1 v_2),
into a result term. The , allows an escape from the Redex DSL into full Racket to
do arbitrary computations, like arithmetic in this case.
With this reduction relation in hand, we can evaluate examples in the language using the
test-->>
unit test form, which will recursively apply the reduction relation until it's done:
(test-->> simple-red-v0 (term (add 3 4)) (term 7))
(test-->> simple-red-v0 (term (if 0 1 2)) (term 2))
These tests will succeed, showing that the first term evaluates to the second in each case.
Unfortunately, this isn't quite enough to evaluate more complex terms:
> (test-->> simple-red-v0 (term (add (if 0 (add 3 4) (add 18 2)) 5)) (term 25))
FAILED ::2666
expected: 25
actual: '(add (if 0 (add 3 4) (add 18 2)) 5)
This is because the reduction relation above is defined for every form in the language, but
it doesn't tell you how to reduce inside nested expressions. For example, there is no
explicit rule for evaluating an if nested inside an add.
Of course, writing rules for all these nested combinations doesn't make sense. That's
where evaluation contexts come in. An evaluation context like E (see the grammar
from earlier) defines where reduction
can happen. Anywhere that a hole exists in an evaluation context is a reducible spot.
So for example, (add 3 hole) and (add hole (if 0 1 2)) are valid evaluation contexts, following
the productions in the grammar.
On the other hand, (if (add 1 -1) hole 5) is not a valid evaluation context, because you can't
evaluate the "then" branch of a conditional before evaluating the condition.
You can combine evaluation contexts with an in-hole form to do context-based matching in
reduction relations. Adding that changes the above reduction relation to this one:
(define simple-red-v1
(reduction-relation simple-language
#:domain e
;; note the in-hole that's added
(--> (in-hole E (add v_1 v_2))
(in-hole E ,(+ (term v_1) (term v_2)))
addition)
(--> (in-hole E (if 1 e_t e_f))
(in-hole E e_t)
if-true)
(--> (in-hole E (if 0 e_t e_f))
(in-hole E e_f)
if-false)))
With this new relation, the test from before will succeed:
(test-->> simple-red-v0 (term (add (if 0 (add 3 4) (add 18 2)) 5)) (term 25))
This is because the in-hole pattern will match an evaluation context whose hole is
substituted with a term that will be reduced.
To make that a bit more concrete, the test above would execute a pattern match like this:
> (redex-match
simple-language
(in-hole E (if 0 e_1 e_2))
(term (add (if 0 (add 3 4) (add 18 2)) 5)))
(list
(match
(list
(bind 'E '(add hole 5))
(bind 'e_1 '(add 3 4))
(bind 'e_2 '(add 18 2)))))
This interaction shows that the evaluation context pattern E gets matched to an add term with a hole.
Inside that hole is an if expression, which is where the reduction will happen.
Evaluation contexts are powerful in that you can describe all of these nested computations with straightforward rules that only mention the inner term that is being reduced. They are also useful for describing more complicated language features as well, such as mutation and state.
With that brief tour of Redex, the next section will give a high-level overview of a model of wasm in Redex.
WebAssembly Design via Redex
WebAssembly is an interesting language because its design goals are specifically oriented towards web programming. That means, for example, that programs should be compact so that web browsers don't have to download and process large scripts.
Security is of course also a major concern on the web, so the language is designed with isolation in mind to ensure that programs cannot access unnecessary state or interfere with the runtime system's data.
The desire for a "a compact program representation" (Hass et al.) led to a stack-based design, in contrast to the simple nested expression language I gave as an example earlier.
This means that operations take values from the stack, rather than nesting
them in a tree-like structure.
For example, instead of an expression like (add 3 4), wasm would use something like
(i32.const 3) (i32.const 4) add. This sequence of instructions pushes two
constants onto the stack, and then performs an addition with values popped from
the stack (and then pushes the result).
Wasm is also statically typed with a very simple type system. The validation provided by the type system ensures that you can statically know the stack layout at any point in the program, which means that you can't have programs that access out-of-bounds positions in the stack (or the wrong registers, if you compile stack accesses to register accesses).
By understanding the semantics, either in math or in model code, you can see how these security concerns are addressed operationally. For example, later in this section I'll explain how the operational semantics demonstrates wasm's memory isolation.
To provide a starting point for explaining the Redex model, here's a screenshot of the grammar of wasm from Hass et al's paper:

This formal grammar can be transcribed straightforwardly as a BNF-style language definition, as explained in the previous section. The grammar in Redex looks something like this:
(define-language wasm-lang
;; basic types
(t ::= t-i t-f)
(t-f ::= f32 f64)
(t-i ::= i32 i64)
;; function types
(tf ::= (-> (t ...) (t ...)))
;; instructions (excerpted)
(e-no-v ::= drop ; drop stack value
select ; select 1 of 2 values
(block tf e*) ; control block
(loop tf e*) ; looping
(if tf e* else e*) ; conditional
(br i) ; branch
(br-if i) ; conditional branch
(call i) ; call (function by index)
(call cl) ; call (a closure)
return ; return from function
(get-local i) ; get local variable
(set-local i) ; set local variable
(label n {e*} e*) ; branch target
(local n {i (v ...)} e*) ; function body instruction
... ; and so on
)
;; instructions including constant values
(e ::= e-no-v
(const t c))
(c ::= number)
;; sequences of instructions
(e* ::= ϵ
(e e*))
;; various kinds of indices
((i j l k m n a o) integer)
;; modules and various other forms omitted
)
This shows just a subset of the grammar, but you can see there's a close correspondence to the math. The main differences are just in the surface syntax, such as how expressions are ordered or nested.
Using this syntax, the addition instructions from before would inhabit the
e* non-terminal for a sequence of instructions. Following the grammar,
it would be written as ((const i32 4) ((const i32 3) (add ε))).
This instruction sequence is represented with a nested
list (where ε is the null list)
rather than a flat sequence to make it easier to manipulate in Redex.
We also need to define evaluation contexts for this language. This is thankfully pretty simple:
(E ::= hole
(v E)
((label n (e*) E) e*))
What these contexts means is that either you will look for a matching
sequence of instructions that comes after a nested prefix (possibly empty)
of values v to reduce, or you will look to reduce inside a label form
(or a combination of these two patterns).
Unlike the simple language from earlier, wasm has side effects, memory, modules, and
other features. Because of this complexity, the machine states of wasm have to
include a store (the non-terminal s), a call frame (F),
a sequence of instructions (e*), and an index for the current module instance
(i).
As a result, the reduction relation becomes more complicated. The structure of the relation looks like this:
(define wasm->
(reduction-relation
wasm-runtime-lang
;; the machine states
#:domain (s F e* i)
;; a subset of reduction rules shown below
;; rule for binary operations, like add or sub
(++> ;; this pattern matches two consts on the stack
(in-hole E ((const t c_1) ((const t c_2) ((binop t) e*))))
;; the two consts are consumed, and replaced with a result const
(in-hole E ((const t c) e*))
;; do-binop is a helper function for executing the operations
(where c (do-binop binop t c_1 c_2))
binop)
;; rule for just dropping a stack value
(++> (in-hole E (v (drop e*))) ; consumes one v = (const t c)
(in-hole E e*) ; return remaining instructions e*
drop)
;; more rules would go here
...
;; shorthand reduction definitions
with
[(--> (s F x i)
(s F y i))
(++> x y)]))
Again, we have the #:domain keyword indicating what the machine states are. Then
there are two rules for binary operations and the drop instruction (other rules
omitted for now).
The rules use a shorthand form ++> (defined at the bottom) that only match
the instruction sequence, and ignores the store, call frame, and so on. This is
just used to simplify how the rules look to match the paper.
For comparison, here's a screenshot of the full reduction semantics figure from the wasm paper:

You can look at the 3rd and 12th rules in that figure and compare them to the two in the code excerpt above. You can see that there's a close correspondence. In this fashion, you can transcribe all the rules from math to code, though you also have to write a significant amount of helper code to implement the side conditions in the rules.
As I promised earlier, by inspecting the semantics, you can see how the
language isolates the memory of wasm scripts that are executing. The store term
s, whose grammar I omitted earlier, is defined like this:
;; stores: contains modules, tables, memories
(s ::= {(inst modinst ...)
(tab tabinst ...)
(mem meminst ...)})
;; modules with a list of closures cl, global values v,
;; table index and memory index
(modinst ::= {(func cl ...) (glob v ...)}
;; tab and mem are optional, hence all these cases
{(func cl ...) (glob v ...) (tab i)}
{(func cl ...) (glob v ...) (mem i)}
{(func cl ...) (glob v ...) (tab i) (mem i)})
;; tables are lists of closures
(tabinst ::= (cl ...))
;; memories are lists of bytes
(meminst ::= (b ...))
The store is a structure containing some module, table, and memory instances. These are basically several kinds of global state that the instructions need to reference to accomplish various non-local operations, such as memory access, global variable access, function calls, and so on.
Each module instance contains a list of functions (stored as closures cl), a
list of global variables, and optionally indices specifying tables and memories
associated with the module.
The functions and global variables have an obvious purpose, which is to allow function calls to fetch the code for the function and allowing global variables to be read/written.
The table index inside modules allow dynamic dispatch to functions stored in a shared table of closures. This lets you use a function pointer-like dispatch pattern without the dangers of pointers into memory.
Finally, each module may declare an associated memory via an index, which means different modules can share access to the same memory if desired.
This index number indexes into the list of memory instances (mem meminst ...),
each of which is just represented as a list of bytes (b ...). The memory can
be used for loads and stores to represent structured data or for other uses of
memory.
The Redex code for memory load and store rules look like this:
;; reductions for operating on memory
(--> ;; one stack argument for address in memory, k
(s F (in-hole E ((const i32 k) ((load t a o) e*))) i)
;; reintrepret bytes as the appropriately typed data
(s F (in-hole E ((const t (const-reinterpret t (b ...))) e*)) i)
;; helper function fetches bytes from appropriate memory in s
(where (b ...) (store-mem s i ,(+ (term k) (term o)) (sizeof t)))
load)
(--> ;; stack arguments for address k and new value c
(s F (in-hole E ((const i32 k) ((const t c) ((store t a o) e*)))) i)
;; installs a new store s_new with the memory changed
(s_new F (in-hole E e*) i)
;; the size in bytes for the given type
(where n (sizeof t))
;; helper function modifies the memory in s, creating s_new
(where s_new (store-mem= s i ,(+ (term k) (term o)) n (bits n t c)))
store)
These rules are a little more complicated and rely on various helper functions. The helper functions are not too complicated, however, and basically just do the appropriate indexing into the store data structure.
One key difference from the earlier rules is the use of --> without any shorthands.
This allows the rules to reference the store s to access parts of the global
machine state. In this case, it's the memory part of the store that's needed.
From this, you can see that wasm code only ever touches the appropriate memory
instance that's associated with the module that the code is in. More
specifically, that's because the store lookup is done using the current module
index i. No other memories can be accessed via this lookup since this index
is fixed for a given function definition.
All memory accesses are also bounds-checked to avoid access to arbitrary
regions of memory that might interfere with the runtime system and result in
security vulnerabilities.
The bounds checking is done inside the store-mem and store-mem= helper
functions, which will fail to match in the where clauses if the index k
is out of bounds.
You can get an idea of how wasm is designed with web security in mind from this particular rule and how the store is designed. If you look at other rules, you can also see how global variables and local variables are kept separate from general memory access as well, which prevents memory access from interfering with variables and vice versa.
In addition, code (e.g., function definitions, indirectly accessed functions in tables) are not stored in the memory either, which prevents arbitrary code execution or modification. You can see this from how the function closures are stored in separate function and table sections in modules, as explained above.
Where to go from here
The last section gave an overview of some interesting parts of the wasm semantics, with a focus on understanding some of the isolation guarantees that the design provides.
This is just a small taste of the full semantics, which you can understand more comprehensively by reading the paper or the execution part of the language specification. The paper's a very interesting read, with lots of attention paid to explaining design rationales.
You can also try examples out with the basic Redex model that I've built, though with the caveat that it's not quite complete. For example, I didn't implement the type system and there are some rough edges around the numeric operations.
There are also interesting ways in which the model could be extended.
For one, it could cover the full semantics that's described in the spec instead of the small version in the paper. If you combined that with a parser for wasm's surface syntax, you could run real wasm programs that a web browser would understand and trace through the reductions.
Wasm's reference interpreter also comes with a lot of tests. With a proper parser, we could feed in all the tests to make sure the model is accurate (I'm sure there are bugs in my model).
It would then be interesting to do random testing to discover if there are discrepancies between the specification-based semantics encoded in the executable model and implementations in various web browsers.
If anyone's interested in exploring any of that, you can check out the code I've written so far on github: https://github.com/takikawa/wasm-redex
Appendix: More Redex Discussion
This section is an appendix of more in-depth discussion about using Redex specifically, if you're interested in some of the nitty-gritty details.
There were several challenges involved in actually modeling wasm in Redex. The first challenge I bumped into is that the wasm model's reduction rules operate on sequences of values, sometimes even producing an empty sequence as a result.
This actually makes encoding into Redex a little tricky, as Redex assumes that evaluation contexts are plugged in with a single datum and not a splicing sequence of them. The solution to this, which you can see in the rules shown above, is to explicitly match over the "remaining" sequence of expressions in the instruction stack and handle it explicitly (either discarding it or appending to it).
Then evaluation contexts can just be plugged with a sequence of instructions or values.
This requires a few cosmetic modifications to the grammar and rules when compared to the paper. For
example, the wasm paper's evaluation contexts simply define a basic context as (v ... hole e ...) in
which the hole could be plugged with a general e ....
Instead, the Redex model uses a context like (v E) where E can a hole or another nesting level.
Then a hole is plugged in with an e* (defined as a list) representing both the thing to plug
into the hole in the original rule plus the "remaining" e ... expressions.
The rules also need to explicitly handle cons-ing and appending of expression
sequences. In a sense, this is just making explicit what was implicit in the
... and juxtaposition in the paper's rules.
Another challenge was the indexed evaluation contexts of the paper. The paper's contexts are indexed by a nesting depth, which constrains the kinds of contexts that a rule can apply to. In Redex it's not possible to add such data-indexed constraints into grammars, so you end up having to apply extra side conditions in the reduction rules where such indexed contexts are used.
For example, this shows in the rule for branching from inside of a control
construct. The evaluation context E below is indexed by a nesting depth k
in the paper's rules:
(==> ((label n {e*_0} (in-hole E ((br j) e*_1))) e*_2)
(e*-append (in-hole E_v e*_0) e*_2)
(where j (label-depth E))
(where (E_outer E_v) (v-split E n))
label-br)
Whereas in the code above, the nesting depth is checked with a metafunction label-depth.
Finally, the reduction relation in wasm has a rule for operating on the local
form (for function invocations), that doesn't follow the structure of typical evaluation
context based reduction.
Specifically, the rule states that when a model state reduces as:
s; v*; e* →_i s'; v'*; e'*,
then you can reduce under a function's local expression as follows:
s; v_0*; local_n {i; v*} e* →_j s'; v_0*; local_n {i; v'*} e'*.
That is, you can reduce under a local if you swap out the call frame and are able to reduce under
the swapped out call frame.
I think this can't be expressed using a normal evaluation context, but it's
still possible to express in Redex as a recursive call to the reduction
relation being defined. Basically, you have to call apply-reduction-relation
on the right-hand side of the rule if you encounter a local form.
To make debugging easier, you also need to use apply-reduction-relation/tag-with-names and
the computed-name form for the rule name to make sure the traces form shows the right
rule names.
Here's what the reduction rule for the local case looks like:
;; specifies how to reduce inside a local/frame instruction via a
;; recursive use of the reduction relation
(--> (s_0 F_0 (in-hole E ((local n {i F_1} e*_0) e*_2)) j)
(s_1 F_0 (in-hole E ((local n {i F_2} e*_1) e*_2)) j)
;; apply --> recursively
(where any_rec
,(apply-reduction-relation/tag-with-names
wasm-> (term (s_0 F_1 e*_0 i))))
;; only apply this rule if this reduction was valid
(side-condition (not (null? (term any_rec))))
;; the relation should be deterministic, so just take the first
(where (string_tag (s_1 F_2 e*_1 i)) ,(first (term any_rec)))
(computed-name (term string_tag)))